实验教学方法
针对传统教学中用二维线条表示三维模型不够直观形象问题（表1，图1），基于晶体学的基本知识（图2），利用ShapeV7.1、Rhino、3Ds Max等软件建立32类点群对称型晶体的三维数字模型（图3）。
表1 晶体的对称分类
| 晶族 | 晶系 | 对称特点 | 对称型 | 对称型符号 | 晶类名称 | |
| 圣弗利斯符号 | 国际符号 | |||||
| 低级晶族 | 三斜晶系 | 无L2，无P | L1 | C1 | 1 | 单面 |
| C | Ci=S2 | 1 | 平行双面 | |||
| 单斜晶系 | L2或P不多于1个 | L2 | C2 | 2 | 轴双面 | |
| P | C1h=Cs | m | 反映双面 | |||
| L2PC | C2h | 2/m | 斜方柱 | |||
| 斜方晶系 | L2或P多于1个 | 3L2 | D2=V | 222 | 斜方四面体 | |
| L22P | C2v | mm2 | 斜方单锥 | |||
| 3L23PC | D2h=Vh | mmm | 斜方双锥 | |||
| 中级晶族 | 四方晶系 | 有一个L4或Li4 | L4 | C4 | 4 | 四方单锥 |
| L42L2 | D4 | 422 | 四方偏方面体 | |||
| L4PC | C4h | 4/m | 四方双锥 | |||
| L4P | C4v | 4mm | 复四方单锥 | |||
| L44L25PC | D4h | 4/mmm | 复四方双锥 | |||
| Li4 | S4 | 4 | 四方四面体 | |||
| Li42L22P | D2d=Vd | 42m | 复四方偏三角面体 | |||
| 三方晶系 | 有1个L3 或Li3 | L3 | C3 | 3 | 三方单锥 | |
| L33L2 | D3 | 32 | 三方偏方面体 | |||
| L3C=Li3 | Ci3=S6 | 3 | 复三方单锥 | |||
| L33P | C3v | 3m | 菱面体 | |||
| L33L23PC=Li33L23P | D3d | 3m | 复三方偏三角面体 | |||
| 中级晶族 | 六方晶系 | 有1个L6 或Li6 | L6 | C6 | 6 | 六方单锥 |
| L66L2 | D6 | 62 | 六方偏方面体 | |||
| L6PC | C6h | 6/m | 六方双锥 | |||
| L66P | C6v | 6mm | 复六方单锥 | |||
| L66L27PC | D6h | 6/mmm | 复六方双锥 | |||
| Li6=L3P | C3h | 6 | 三方双锥 | |||
| Li63L23P=L33L24P | D3h | 62m | 复三方双锥 | |||
| 高级晶族 | 等轴晶系 | 有4个L3 | 3L24L3 | T | 23 | 五角三四面体 |
| 3L24L33PC | Th | m3 | 偏方复十二面体 | |||
| 3Li44L36P | Td | 43m | 六四面体 | |||
| 3L44L36L2 | O | 43 | 五角三八面体 | |||
| 3L44L36L29PC | Oh | m3m | 六八面体 | |||
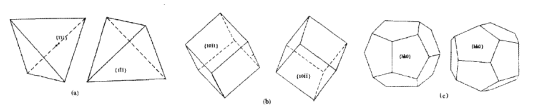
图1 传统教学中的二维模型
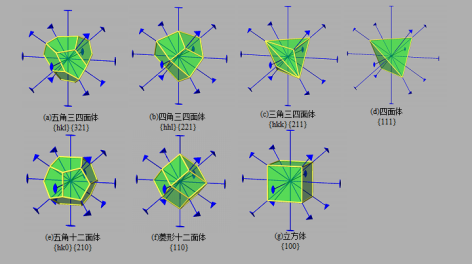
图2 等轴晶体推导
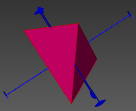
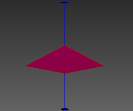
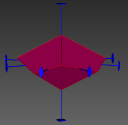
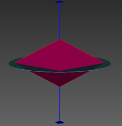
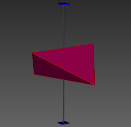
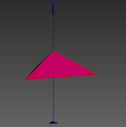
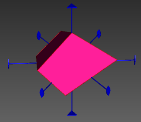
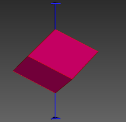
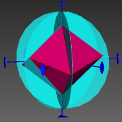
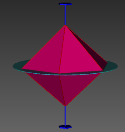
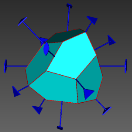
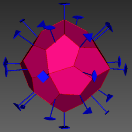
图3 晶体结构3D数字模型
同济大学基础地质虚拟实验课程版权所有